Литература: Кормен и Co. Алгоритмы. Построение и анализ.
Справочные материалы: Вики-конспекты ИТМО
Визуализаторы: rain.ifmo.ru
Крайне любопытная структура данных, на основе которой можно организовать приоритетную очередь.
Ниже представлена асимптотическая сложность базовых операций:
1. Добавление нового элемента O(1)
2. Определение минимального элемента O(1)
3. Слияние двух фибоначчиевых куч O(1)
4. Удаление минимального элемента O(logN)
5. Изменение приоритета элемента O(logN)
Фибоначчиева куча представляет собой набор фибоначчиевых деревьев.
Фибоначчиево дерево представляют собой k-ричное дерево для которого существует только одно правило: сын не должен превышать своего отца.
Братья-узлы объединены в кольцевой список. Поэтому отцу не обязательно знать всех сыновей. Достаточно иметь ссылочку на одного из них. Минимальный элемент всей кучи – это корень одного из деревьев. Ниже представлен пример фибоначчиевой кучи.
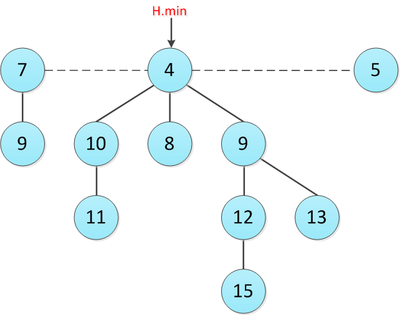
Программно будем хранить узел фибоначчиева дерева и саму фибоначчиеву кучу так:
- typedef bool (*cmpPtr)(node*, node*);
- struct node {
- node* parent; // указатель на отца
- node* child; // указатель на одного из сыновей
- node* left; // указатель на левого брата
- node* right; // указатель на правого брата
- int degree; // количество дочерних узлов
- bool mark; // метка - был ли удален один из дочерних элементов
- int key; // числовое значение узла
- };
- struct fib_heap {
- node* min; // узел с минимальным корнем
- int roots_amount; // количество узлов
- cmpPtr less; // указатель на функцию-компаратор
- }
* This source code was highlighted with Source Code Highlighter.
Рассмотрим работу алгоритма на конкретном примере. Последовательно будет добавлять элементы из массива:
{5,1,3,2,4,0,7,6}
1. Добавление элемента
 | В начальный момент куча пуста и нет ни одного дерева. Новый элемент “5” становится корнем единственного дерева и одновременно минимальным элементом всей кучи. |
 | Элемент “1” образует новое дерево и отбирает титул минимального элемента кучи у “5”. Каждый новый добавленный элемент будет образовывать новую дерево, а его корень будет добавляться в кольцевой список корней. |
 | Элемент “3” добавляется справа от минимального элемента. |
 | Элемент “2” не меняет минимальный элемент кучи и как и элемент “3” встает справа от минимального корня. |
 | Элемент “1” повторяет судьбу “2” |
 | Элемент “0” становится новым минимальным элементом кучи и также добавляется справа от предыдущего минимального элемента |
 | |
 |
Программно функция добавления нового элемента может выглядеть так:
- void add(node* Node, node** bro, node* par = NULL) {
- if (*bro == NULL) {
- *bro = Node;
- Node->left = Node;
- Node->right = Node;
- }
- else {
- Node->right = (*bro)->right;
- Node->right->left = Node;
- Node->left = *bro;
- (*bro)->right = Node;
- }
- if (less(Node, *bro))
- *bro = Node;
- if(*bro == min) {
- roots_amount++;
- Node->parent = NULL;
- }
- if (par){
- par->degree++;
- Node->parent = par;
- }
- }
- node* add(int key) {
- node* Node = new node(key);
- add(Node,&min);
- return Node;
- }
* This source code was highlighted with Source Code Highlighter.2. Определение минимального элемента
Указатель на минимальный элемент кучи хранится в специальном поле. Доступ к нему осуществляется за O(1)
3. Объединение двух фибоначчиевых куч
То, что эта функция работает за константное время выгодно отличает фибоначчиеву кучу от биномиальной и двоичной, где время работы пропорционально O(logN) и O(NlogN).
Т.к. корневые узлы объединены в циклический список, то для объединения двух куч необходимо объединить два циклических списка корней в один. Это можно сделать за константное время путем аккуратного перекидывания ссылок:
- struct fib_heap {
- void union_fib_heap(fib_heap &fb) {
- union_root(fb.min,fb.roots_amount);
- if (!min || (fb.min && less(fb.min, min)))
- min = fb.min;
- fb.clear();
- }
- void union_root(node* Node, int nodes_amount) {
- if (Node == NULL) return;
- if (min == NULL) {
- min = Node;
- roots_amount = nodes_amount;
- }
- else {
- node *L = Node->left;
- node *R = min->right;
- min->right = Node;
- Node->left = min;
- L->right = R;
- R->left = L;
- roots_amount += nodes_amount;
- }
- }
- };
-
- int main() {
- fib_heap fh1,fh2;
- ...
- fh1.union_fib_heap(fh2);
- ...
- }
* This source code was highlighted with Source Code Highlighter.4. Удаление минимального элемента
Эта операция является наиболее трудоемкой. Поэтому ее описание разобьем на несколько этапов:
4.1. Если минимальный элемент имеет детей, то их необходимо сделать корневыми узлами. В этом может помочь функция union_root, рассмотренная ранее. Этот момент будет проиллюстрирован чуть позже.
4.2. Удаляем минимальный элемент из кольцевого списка корней. Для этого нужно грамотно перебросить ссылочки с левого и правого брата. При этом новым минимальным элементом кучи на время становится правый брат удаляемого элемента. Не факт, что правый брат является минимальным узлом, но после окончания функции будет найден корректный минимальный узел. Может возникнуть такая ситуация, что удаляемый элемент является последним элементов в кольцевом списке. Этот случай наступит, когда min->right == min и его нужно обработать отдельно. В случае, когда удаляемый элемент не является последним, то нужно выполнить процесс уплотнения кучи(consolidate):
- int extract_min() {
- node* res = min;
- if (res) {
- childs_in_root(res);
- remove_root(res);
- if (res->right == res)
- min = 0;
- else {
- min = min->right;
- consolidate();
- }
- }
- int ans = res ? res->key : ERROR;
- delete res;
- return ans;
- }
* This source code was highlighted with Source Code Highlighter. 4.3. Процесс уплотнения кучи(consolidate) лучше понять на иллюстрации кучи, которую мы получили на этапе процесса добавления новых элементов. На каждом шаге будут формироваться новые фибоначчиевы деревья размером равным степени двойки. Если на каком-то этапе получается два дерева одинакового размера они объединяются в одно и так повторяется до тех пор пока в наборе остаются деревья одинакового размера.
 | После удаления минимального элемента “1” текущим элементом становится правый его брат “6”, образую первое фибоначчиево дерево размером 1. |
 | Переходим к правому брату элемента “6”, т.к. к “7”, который образует дерево размером 1. Но на предыдущем шаге уже было получено дерево с таким размером. Объединяем их |
 | При слиянии двух деревьев “6” и “7” минимальный корень двух деревьев становится общим корнем. А корень второго дерева становится сыном общего корня. После чего образуется новое дерево размером 2 – “6-7”. Увеличиваем счетчик детей у элемента “2”. |
 | Следующим элементом становится “4”, образуя дерево размером 1. На текущем шаге имеется одно дерево размером 2 и одно дерево размером 1. Поэтому сливать деревья не надо |
 | Новое дерево “2” имеет тот же размер, что и дерево “4”. Сливаем их. |
 | После слияния получается дерево “2-4” размером 2. Но у нас уже есть дерево размером 2 – “6-7”. Поэтому сливаем сливаем эти деревья |
 | При слиянии деревьев на предыдущем шаге образуется дерево размером 4, корнем которого является элемент “2”. Элемент “6” становится сыном элемента “2”. На рисунке нет явной связи “2” и “6”, потому что “6” включена в циклический список с “4”, который является сыном “2”. |
 | Новый дерево “3” имеет уникальную размерность |
 | Далее рассуждения можно продолжить по аналогии с предыдущими шагами. |
 | |
 | В итоге получаются 3 дерева уникального размера. Все корни циклического списка, который был вначале обработаны. На этом шаге процесс уплотнения кучи закончен. Отметим, что на текущем шаге уже известен минимальный корень кучи. Он определяется каждый раз, когда образуется дерево уникального размера. |
Давайте теперь более детально разберем, что происходит в п. 4.1 и 4.2. Допустим, что на текущий момент уже удален минимальный элемент “1” и мы имеем:
 | Минимальным элементом кучи является 2. |
 | В п.4.1. сказано, что нужно детей минимального элемента поместить в корневой список кучи, что мы и делаем. Далее элемент “2” удаляется и происходит сжатие кучи по вышеописанной схеме. |
5. Изменение приоритета элемента
Осталась последняя операция, которую мы разберем. Очевидно, если новый приоритет элемента не ниже, чем приоритет его отца, то ничего делать не нужно. В противном случае действует по следующей схеме:
5.1. Удаляем текущий элемент A из кольцевого списка братьев и если отец A(P) ссылался на этот элемент A, то перебрасываем ссылку child элемента P на правого брата A. Уменьшаем счетчик количества сыновей у P и делаем метку mark равную true. Это означет, что у элемента P был удален сын. Данная метка указывает на то, что если возникнет такая ситуация, что у одного узла будет удалено более одного сына, то его нужно поместить в кольцевой список корней.
5.2 Добавляем элемент A в кольцевой список корней. Если приоритет элемента A меньше минимального корня, то элемент A становится минимальным элементом кучи.
5.3. Делаем каскадное вырезание. То, о чем идет речь в п.5.1. Если у отца элемента A – элемента P ранее удалялся сын, то необходимо выполнить поместить элемент P в кольцевой список корней. Далее продолжить п.5.3. для отца элемента P, если у него также ранее удалялись сыновья.
Задача: EZDIJKST
Решение: здесь
Примечание: полная реализация фибоначчиевой кучи

